728x90

이러한 행렬의 곱은 공학수학이나 이산수학에서 충분히 배웠다. 이때 Aik, b kj로 k가 왼쪽 식에는 오른쪽에, 오른쪽은 왼쪽에 적혀 있는건 두개가 같을 경우에 연산이 되기 때문이다.
분할 정복의 아이디어로는 다음과 같다.


// r 배열은 행렬들의 행과 열의 수를 저장
// i부터 j까지의 행렬을 곱할 때 최소 곱셈 횟수를 반환하는 함수
public static int matMult_DC(int[] r, int i, int j) {
// 기저 조건: 행렬이 하나일 경우 곱셈이 필요하지 않음
if (i == j) return 0;
int minVal = Integer.MAX_VALUE; // 최소 곱셈 횟수를 무한대 값으로 초기화
// i부터 j-1까지의 k를 기준으로 분할하여 최소 곱셈 횟수를 계산
for (int k = i; k < j; k++) {
int count = matMult_DC(r, i, k)
+ matMult_DC(r, k + 1, j)
+ r[i - 1] * r[k] * r[j]; // 분할한 두 부분의 곱셈 횟수와 현재 부분 곱셈 횟수 합산
minVal = Math.min(minVal, count); // 최소 곱셈 횟수 갱신
}
return minVal; // 최종 최소 곱셈 횟수 반환
}동적 계획 알고리즘으로 행렬.
n행렬 곱셈들의 순서
행렬곱의 수( h )
0 matMult(1, 1) matMult(2, 2) . . . matMult(n-2, n-2) matMult(n-1, n-1) matMult(n, n)
1 matMult(1, 2) matMult(2, 3) . . . matMult(n-2, n-1) matMult(n-1, n)
2 matMult(1, 3) matMult(2, 4) . . . matMult(n-2, n)
.
.
.
n-2 matMult(1, n-1) matMult(2, n)
n-1 matMult(1, n)
nmatMult(i, j) = MIN┬(i≤k<j)〖"(" matMult(i, k)+matMult(k+1,j)+r_(i-1) r_k r_j " )" 〗 , 1≤i≤n-h , j = i + h
matMult(i, j) = 0, i = j
n주: matMult(1 . . n)의 값은 배열 m[1..n, 1..n]에 저장한다.
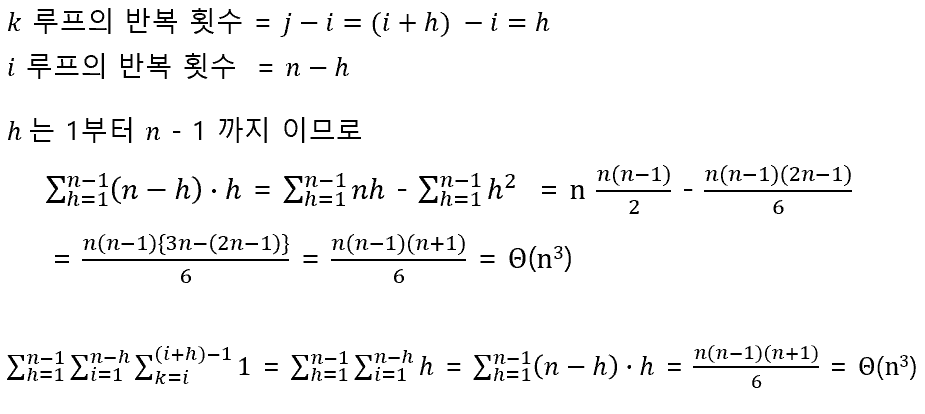



728x90
'알고리즘' 카테고리의 다른 글
| 되추적 ( Backtracking) (0) | 2024.11.26 |
|---|---|
| 동적 계획 (Dynamic Programming) 알고리즘 (0) | 2024.11.02 |
| 분할 정복(Divide and Conquer) (0) | 2024.11.02 |